August 24, 2016

Benford’s Law

I don’t know much about probability or statistics or any of that mathematical stuff, and I don’t really care much to know either, but Benford’s Law is some really cool stuff and I’m excited to tell you all about it in this blog post.

Alright, so back in the year 2001, there was this huge company worth around $70 billion dollars. $90 per share. That company was Enron, and it was known as the darling of Wall Street, the kings of the stock market. Now, let me further clarify how much $70 billion dollars really is.

Multiply that image by 70. Now that’s straight bank. So where did all of the money go? It went spiralling down in October 2001, after a couple of Enron’s executives, including their own founder and CEO, were indicted and convicted for 19 counts of conspiracy, fraud, false statements and insider trading.

Yeah. America’s most innovative company. 19 counts of fraud and insider trading. What a surprise, right?

So what happened, really? #

Enron’s accountants basically falsified a bunch of numbers in their income reports. They admitted to misstating their income and the equity value for the company was a couple of billion dollars less than its balance sheet said. That is actually crazy.

So Enron declared bankruptcy, thousands of people lost their jobs, thousands of investors lost billions of dollars as Enron’s beautiful $90 per share shrank to penny-stock levels.

How were they caught? #

Three words. Benford’s Law, baby. We all know what laws are, they’re like established rules and algorithms on how something works. The Laws of Physics for example, that’s how physics work and that’s how it will always work.

Well, there’s a law for numbers in datasets. The first digit of those numbers in those datasets, actually. The law is pretty simple: in most datasets, the first digit of every number appears to be one 30.1% of the time, and 9 about five percent of the time. In mostly every scenario, this is always the case.

Take electricity bills, street addresses, stock prices, house prices, population numbers, death rates, lengths of rives, income reports, and census data, and you will find that the first digit of every number in the dataset is in fact one, from a range between 28% to 32%.

When I typed that last paragraph, I mentioned that even census data follows Benford’s Law. I wasn’t entirely sure about that, so I decided to go ahead and test it for those of you reading, so that you could see the true power of this.

I wrote the below code in Ruby by the way, which is completely unorthodox of me, but I felt like I finally needed to give Ruby a chance, at least when it comes to data analysis (even though Python is a clear winner in that regard).

First we need to require the CSV gem, since our dataset, like most datasets, are generated in the CSV format. Let’s go ahead and do that.

require 'csv'

Now it’s time to write the method that will take our dataset and the position of the numbers we are trying to test Benford’s Law against.

def benford_law(csv_file, position)
    first_digits = Array.new(10, 0)
    CSV.foreach(csv_file) do |row|
        digit = row[position].to_s[0]
        first_digits[digit.to_i] += 1  if digit =~ /[0-9]/
    end
    first_digits
end

This method is basically taking all of the numbers and getting the count of the first digit of each of those numbers by calling index 0. Simple enough, right?

Great, so now let’s call on our method and make sure it’s formatted neatly and appropriately!

first_digits = benford_law("census.csv", 4)
total = first_digits.inject(0) do |sum, v| 
  sum + v 
end

puts "Percentages of the first digits"
puts "-" * 50
first_digits.each_with_index do |v, i| 
  puts "#{i} => #{ ((v.to_f / total.to_f) * 100.0).to_s[0..4]} " if i != 0
end

You should now have all of the code you need to test Benford Law’s against the dataset of the Census in 2010. Let’s run this code and see our output.

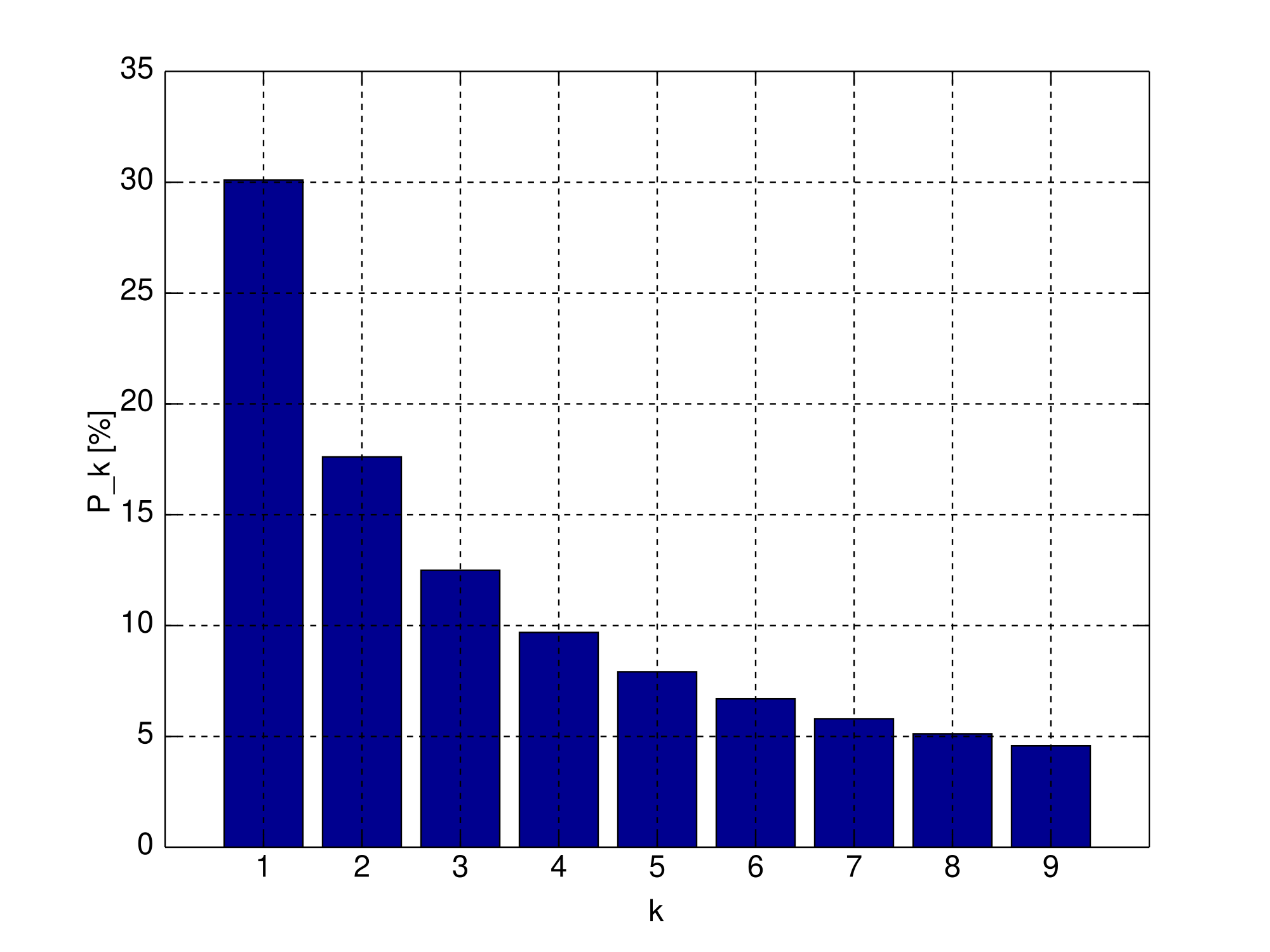
Percentages of the first digits
--------------------------------------------------
1 => 30.32 
2 => 18.89 
3 => 11.89 
4 => 9.799 
5 => 6.776 
6 => 6.713 
7 => 5.790 
8 => 4.836 
9 => 4.963

Woah, do you see what’s happening here? Benford Law is proven to be true. 1 is the first digit 30% of the time, while 9 is the first digit only 5% of the time. This is exactly what the rule states. Isn’t that so crazy?

So is this how Enron was caught? #

This is exactly how Enron was caught. Benford’s Law seems really simple, but it certainly isn’t intuition. The accountants at Enron were told to write random numbers to that they could seem more valuable than they were, but what these accountants obviously didn’t take into account (pun intended) was the possibility of there existing a law around the distribution of first digits.

Which led to them writing a bunch of random numbers. The SEC looked into it and they saw that 1 wasn’t the first-digit 28% to 32% of the time, it was incredibly off, so they started investigating. Eventually, their investigations led into them realizing that it was all bullshit.

How does Benford’s Law work? #

Well, it seems pretty logical, doesn’t it? The first digit in a dataset of the population of countries in the world will be 1 more than any other number because it’s easier to get to 1. For example, it’s easier for a country to have 100 million people as opposed to 900 million people. The increase from 100 million to 200 million is 100%, but the increase from 900 million to 1 billion is only 10%.

1 will always be easier to reach, and it will always take a long time to be at because it’s harder to reach to the start of a greater number.

Conclusion #

I would have loved to plot a graph on the Census demo we created a bit earlier, but since I was using Ruby, I couldn’t. Python has a library called matplotlib which allows you to easily plot your dataset. Ruby literally has no equivalent. That’s unfortunate, but it leads me to my next line.

To Yukihiro Matsumoto: Support data science, dude!

Kudos